1. Autotuner整体结构 一开始尝试了OpenTuner 的使用,安装后也成功运行了示例。在了解project1的需求后,决定尝试自己实现一个Autotuner测试MatrixMultiplication.c程序的可配置参数,根据性能选择最优配置输出。
使用Python进行项目搭建。
(1) 文件树 所有项目代码结构如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 . │ Autotuner.py----------------------Autotuner主程序 │ input.txt-------------------------所有输入信息(目标程序、参数组合、参数搜索算法) │ MatrixMultiplication.c------------被测试程序 │ test.py---------------------------执行测试程序,调用Autotuner接口 │ testCounter.txt-------------------记录test的次数,每次测试创建新的测试结果文件夹 │ ├─codes------------------------------代码文件夹 │ ├─input-----------------------------输入模块 │ │ InputDealer.py-----------------处理用户的三种输入 │ │ │ ├─runners---------------------------执行模块 │ │ └─C_runner-------------------------C语言程序执行模块 │ │ C_runner.py-------------------C语言程序执行程序 │ │ │ └─search_algs-----------------------参数搜索模块 │ allAlgs.py--------------------综合处理所有搜索算法 │ GreedySearch.py---------------贪心搜索算法程序 │ GridSearch.py-----------------网格搜索算法程序 │ ├─result-----------------------------测试结果文件夹 ├─test1------------------------------测试结果1 │ │ program.c------------------------复制过来的被测程序 │ │ result.txt-----------------------测试结果 │ │ │ └─tmp-----------------------------编译产生的临时文件夹 │ out.txt---------------------获取被测文件的输出,写入其中 │ tmp.exe---------------------编译生成的可执行文件 │ └─test2 │ program.c │ result.txt │ └─tmp out.txt tmp.exe
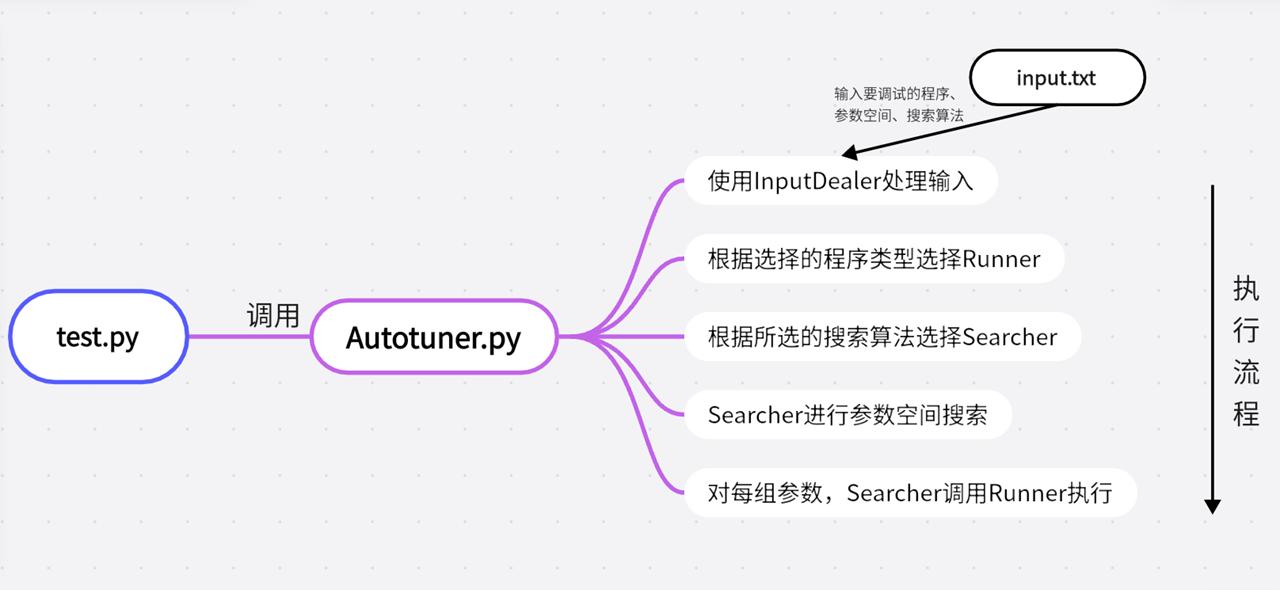
(2) 项目结构 整个测试过程的流程图如下所示:
详细流程:
test.py调用Autotuner.py的相关接口,执行Autotuner.test()方法开始测试。
Autotuner首先调用InputDealer处理用户的输入。
然后根据被测程序的后缀名选择合适的Runner(.c用C_runner, .py用Py_runner, .java用Java_runner等)。
再根据选择的搜索算法,调用对应的Searcher。
Searcher内部调用Runner,提供参数的同时获得Runner的反馈,执行其参数搜索算法。
最后Searcher给出最优性能的参数组合。
整个InputDealer获取参数的详细过程如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 ----------------------------Autotuner---------------------------- Input the program, parameters combination and searching algorithm, then test the program to search the best combination of parameters. Absolute address of program: E:\_files\MajorLessons\软件系统优化\project\p1\project\ MatrixMultiplication.c Please input the compiling parameters: Parameters: `Type '\example' to view an example `Type '\end' to end input param1 name :optimize_level values :O0,O1,O2,O3 param2 name :\end Please input the running parameters: Parameters: `Type '\example' to view an example `Type '\end' to end input param1 name :block_size values :8,16,32,64,128 param2 name :\end Supported algorithms: 1. Grid Search 2. Greedy Search Input the number of algorithm to choose it: 1 Algorithm: Grid Search has been chosed. Running parameters combination: {optimize_level: O0} {block_size: 8} ...
先后采集四种参数:
被测程序的绝对路径
编译参数空间
运行参数空间
参数搜索算法
能够处理多个编译参数和运行参数。
为方便起见,在test.py中将stdin重定向为input.txt。
input.txt:
1 2 3 4 5 6 7 8 9 E:\_files\MajorLessons\软件系统优化\project\p1\project\MatrixMultiplication.c optimize_level O0,O1,O2,O3 \end block_size 8,16,32,64,128 \end 1
得到参数后,将其返回给Autotuner对象。
(4) Searcher 用编译参数、运行参数、runner以及测试次数iters初始化Searcher。每个Searcher必须有一个search方法,作为Autotuner搜索参数组合的接口。然后所有Searcher的信息保存在allAlgs.py中,维护一个Searcher Map:
1 2 3 4 5 6 7 8 9 10 11 12 from .GridSearch import GridSearchfrom .GreedySearch import GreedySearchALGS_LIST = [ 'Grid Search' , 'Greedy Search' , ] algs_dict = { ALGS_LIST[0 ]: GridSearch, ALGS_LIST[1 ]: GreedySearch }
Searcher.search()方法产生参数组合: 编译参数组合和运行参数组合,传给runnner运行,并从runnner获得反馈。
(5) Runner 不同的Runner用以运行不同语言的程序,Runner有一个.run()方法,获取编译参数和运行参数(若该程序没有编译阶段,则编译参数为None)。
2. 实现的优劣 (1) 优势
各个模块间耦合度低,模块与模块之间的交流基本只涉及一个接口,其余工作都在模块内部实现,这样使得代码可读性和可延展性很强。
结构的可扩展性很强。若要增加被测程序的类型,添加一个Runner即可;若要添加搜索算法,添加一个Searcher并加入map即可。
能满足多参数搜索。在InputDealer处也可看出,输入的参数可以不止一种,编译参数可以是多种,运行参数也可以是多种。
多次测试会生成不同的文件夹(参考了specjvm2008的result形式),每次测试在单独的文件夹中进行,互不干扰。
(2) 劣势
未使用多线程运行测试,可能会导致效率低下。opentuner是采用多线程进行测试的。
用户接口可能过于冗杂。但是考虑到需要输入目标程序,不得不使用这种形式。opentuner是将待测程序直接放在代码中。
3. Greedy Search 我自行设计了一种参数搜索算法,命名为“贪心搜索算法”,但在一定程度上,我更愿意叫他梯度下降搜索算法。下面展示其思想。
**Greedy Search执行的流程: **
随机选取一种参数组合,并测试,得到测试时间。
访问该参数组合的邻域,并对领域的每种组合进行测试。
在邻域的所有测试结果中选择一个时间最短的,然后将当前参数组合改为该参数组合。
重复2,3步,直到当前参数组合耗时为其邻域内耗时最短的,退出,并认为当前参数组合为最优参数组合。
名词解释:
**邻域: ** 保持其他参数不变,只前后改变一种参数,并只在左右1格的范围内改变。如:当前参数组合为{optimize level: O2, block size: 16},则其邻域为:
optimize level: O1, block size: 16
optimize level: O3, block size: 16
optimize level: O2, block size: 8
optimize level: O2, block size: 32
当然,在搜索的过程中,会检查该邻域是否访问过了。若已经访问过,则会跳过。因为当前选择的参数组合不是邻域参数组合,说明当前参数组合的运行时间要比邻域的短,所以甚至不用访问该邻域的运行时间,直接跳过即可。
用图像来解释即为:
这种访问邻域然后选择最优的点进入,有些类似函数空间上的梯度下降,但并不准确,因此我称其为贪心搜索算法。
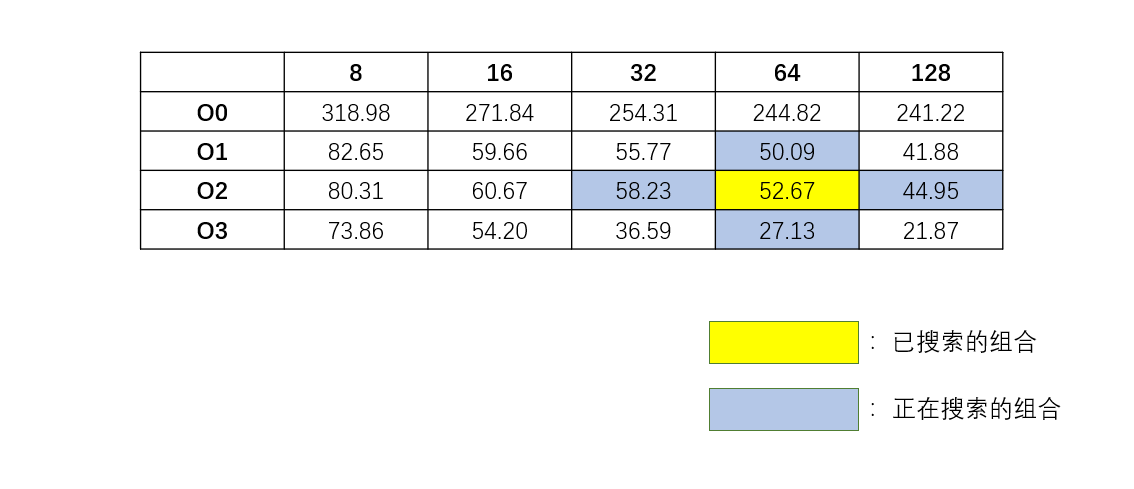
4. Grid Search和Greedy Search的比较 (1) 运行效率 **Grid Search: **
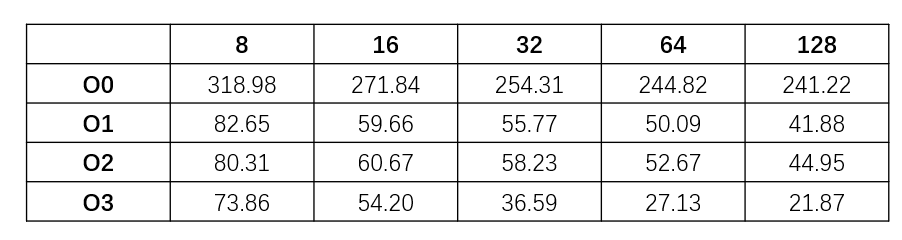
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 Algorithm: Grid Search has been chosed. Running parameters combination: {optimize_level: O0} {block_size: 8} Average time cost: 318.987372s Running parameters combination: {optimize_level: O0} {block_size: 16} Average time cost: 271.838465s Running parameters combination: {optimize_level: O0} {block_size: 32} Average time cost: 254.311087s Running parameters combination: {optimize_level: O0} {block_size: 64} Average time cost: 244.821887s Running parameters combination: {optimize_level: O0} {block_size: 128} Average time cost: 241.217270s Running parameters combination: {optimize_level: O1} {block_size: 8} Average time cost: 82.647090s Running parameters combination: {optimize_level: O1} {block_size: 16} Average time cost: 59.657127s Running parameters combination: {optimize_level: O1} {block_size: 32} Average time cost: 55.773572s Running parameters combination: {optimize_level: O1} {block_size: 64} Average time cost: 50.092287s Running parameters combination: {optimize_level: O1} {block_size: 128} Average time cost: 41.875394s Running parameters combination: {optimize_level: O2} {block_size: 8} Average time cost: 80.311958s Running parameters combination: {optimize_level: O2} {block_size: 16} Average time cost: 60.672041s Running parameters combination: {optimize_level: O2} {block_size: 32} Average time cost: 58.227193s Running parameters combination: {optimize_level: O2} {block_size: 64} Average time cost: 52.674716s Running parameters combination: {optimize_level: O2} {block_size: 128} Average time cost: 44.953127s Running parameters combination: {optimize_level: O3} {block_size: 8} Average time cost: 73.855066s Running parameters combination: {optimize_level: O3} {block_size: 16} Average time cost: 54.200823s Running parameters combination: {optimize_level: O3} {block_size: 32} Average time cost: 36.591904s Running parameters combination: {optimize_level: O3} {block_size: 64} Average time cost: 27.134263s Running parameters combination: {optimize_level: O3} {block_size: 128} Average time cost: 21.869392s Best combination: optimize_level: O3 block_size: 128 Average time cost: 21.869392 Total time of the experiment: 10740.233052s
**Greedy Search: **
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 Algorithm: Greedy Search has been chosed. Running parameters combination: {optimize_level: O2} {block_size: 64} Average time cost: 57.523089s Running parameters combination: {optimize_level: O1} {block_size: 64} Average time cost: 50.706293s Running parameters combination: {optimize_level: O3} {block_size: 64} Average time cost: 27.557757s Running parameters combination: {optimize_level: O2} {block_size: 32} Average time cost: 59.431044s Running parameters combination: {optimize_level: O2} {block_size: 128} Average time cost: 48.006461s Running parameters combination: {optimize_level: O3} {block_size: 32} Average time cost: 37.255367s Running parameters combination: {optimize_level: O3} {block_size: 128} Average time cost: 22.398077s Best combination: optimize_level: O3 block_size: 128 Average time cost: 22.398077 Total time of the experiment: 1542.825604s
差异显而易见。Greedy Search的搜索空间(7种组合)较Grid Search的搜索空间(20种组合)要小很多,整体运行时间也差异很大,Grid Search的搜索时间是Greedy Search的6倍多。并且Greedy Search也成功找到了正确的最优组合。
Greedy Search的运行效率一定程度上取决于初始点的选择。这次运气比较好,选择的初始点离最终点比较近。若初始点选为了{O0, 8},可能耗时会大很多,但是必然低于Grid Search。
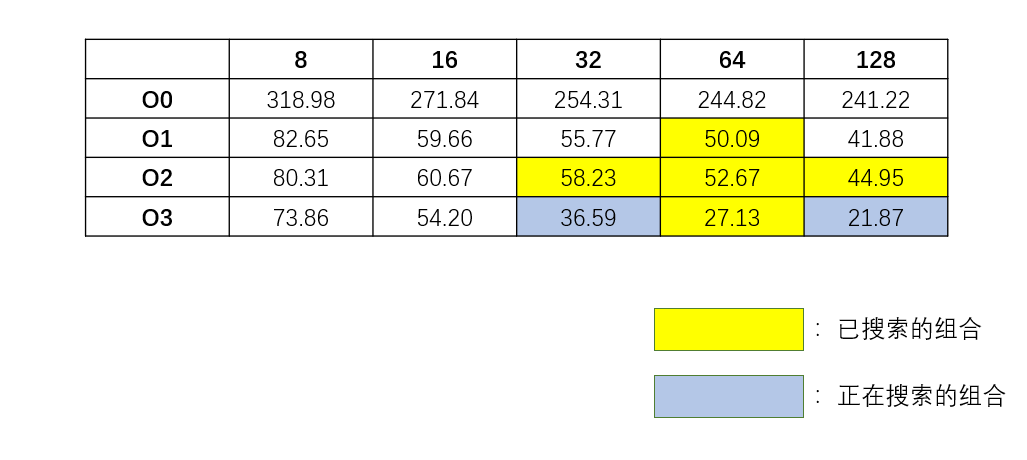
(2) 结果准确性 虽然上面的结果显示Greedy Search找到了全局最优的参数组合,但是这并不是一种必然。上面提到过,Greedy Search的搜索方法类似于梯度下降法,因此很容易陷入局部最优点。因此Greedy Search提供的结果不一定是全局最优点。Grid Search的搜索结果如下:
显然,{O1, 128}就是一个局部最优点,因此若初始点变化一下,最终结果就有可能陷入局部最优点,从而给出一个错误的答案。
而比较起来,Grid Search给出的结果是一个全局最优的,而且是必然的。
(3) 算法改进 从两种算法的分析比较来看,Greedy Search可以做以下改进,一定程度上减小其进入局部最优点的概率。
一开始随机选取的参数组合从1个变为多个,并且要尽可能覆盖整个参数空间。然后从这些参数组合中选择最优的参数组合,以其为起点进行Greedy Search。这样能减小陷入局部最小点的概率。
邻域可以从$n^2$个组合变为$n^3$,其中$n$为所有参数的种类数。在上面的参数组合的情况,即邻域从上,下,左,右的4个组合变为上,下,左,右,左上,右上,左下,右下8种组合,这样虽然每次的搜索范围变大了,但是可以更快地下降到局部最优点,并且搜索范围也更全面,不易错过全局最优点。
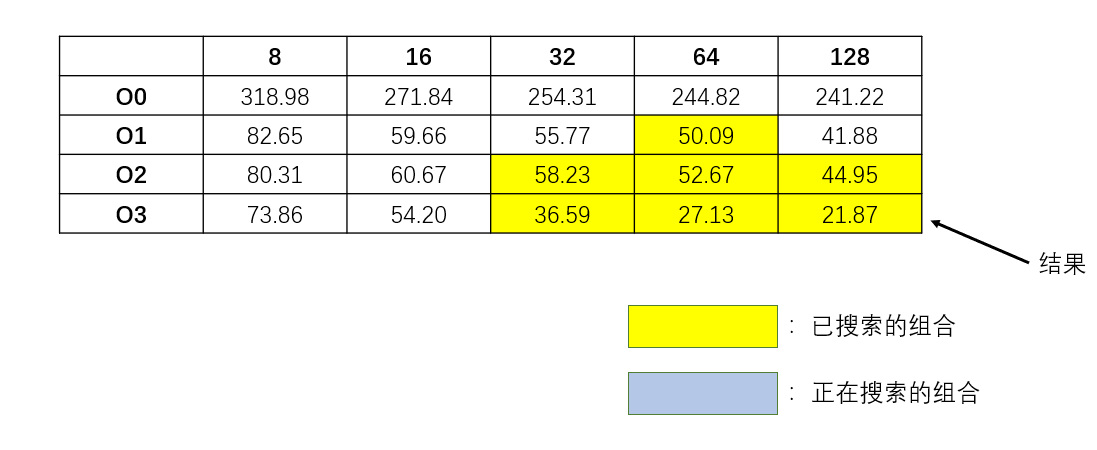
5. 结果分析 所有参数组合的结果如图所示:
(1) Block Size越大,程序运行效率越快 对于每个优化等级,显然Block Size取得越大,程序运行的时间越短。改变Block Size实际上是在改变访问对缓存的读取模式。由于MatrixMultiply.c的数组大小是4096*4096的,显然不可能把所有数值都存进内存。因此数组元素的访问必然涉及磁盘的读写。而改变Block Size可以改变对缓存的读取模式。Block Size越大,缓存页的使用就越充分(前提是Block Size没有超过缓存页的大小),因此缓存使用越充分,程序运行的效率就越高。
(2) 优化等级影响 首先,O0优化等级和其他优化等级程序的差异是显著的,因此无论何种等级的优化,较之无优化程序都能提升一定效率(单就这个程序来说)。
O1: 尝试减少代码大小,缩短代码执行时间,不会执行需要消耗大量编译时间的优化。对于大函数的编译优化会占用更多的时间和内存。
O2: 与-O1类似,会提升编译时间和代码性能,几乎开启除了时空权衡优化外的所有优化项
O3: 在-O2级别的基础上,开启了更多的优化项,最高优化等级,以编译时间、代码大小、内存为代价获取更高的性能。在部分情况下可能会降低性能。
O1 通俗来说,O1优化可以省略一些必然性的计算,比如:
会被优化为:
对于矩阵乘法,一些必然性的加法乘法会被直接优化,减少运算量,因此大大增大了效率。
O2 而到了O2优化,可以明显发现,大部分Block Size使用了O2优化后,效率与O1优化相差无几,甚至还低于O1优化。我搜索了一下,发现O2优化打开了这个选项:
1 -fforce-mem:在做算术操作前,强制将内存数据copy到寄存器中以后再执行。这会使所有的内存引用潜在的共同表达式,进而产出更高效的代码,当没有共同的子表达式时,指令合并将排出个别的寄存器载入。这种优化对于只涉及单一指令的变量, 这样也许不会有很大的优化效果. 但是对于在很多指令(必须数学操作)中都涉及到的变量来说, 这会时很显著的优化, 因为和访问内存中的值相比,处理器访问寄存器中的值要快的多。
对于单变量涉及多计算时,这个优化效率很明显,但是对于频繁访问内存的矩阵乘法来说,该优化可能效果并不明显,甚至会让效率降低。
O3 O3优化的效率要显著优于前两种优化。尤其是在Block Size更大的时候。似乎Block Size越大,O3的效果越明显。我搜索到了相关的优化内容:
1 2 3 -fweb:构建用于保存变量的伪寄存器网络。 伪寄存器包含数据, 就像他们是寄存器一样, 但是可以使用各种其他优化技术进行优化, 比如cse和loop优化技术。这种优化会使得调试变得更加的不可能,因为变量不再存放于原本的寄存器中。 -frename-registers:在寄存器分配后,通过使用registers left over来避免预定代码中的虚假依赖。这会使调试变得非常困难,因为变量不再存放于原本的寄存器中了。
这两者针对的是变量的访问,对于矩阵乘法来说,要反复存取矩阵中的变量,因此该优化能显著提升效率。至于其优化效果随着Block Size的变大而增强,我猜测是伪寄存器访问缓存的效率越来越高。